Textile Statistics: The mean yarn count of 200 samples is 20.46 Ne, and the standard deviation is 0.5. The tolerance limit for yarn count variation is 19.7 Ne to 21.22 Ne. Determine the off-count percentage.

To determine the off-count percentage, we need to find the proportion of samples that fall outside the tolerance limits.
First, let’s find the z-scores corresponding to the lower and upper tolerance limits:
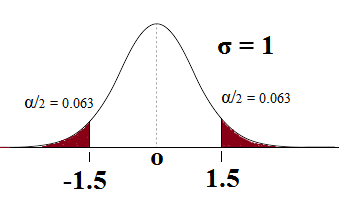
For the lower limit (19.7 Ne):
Z_Lower = (19.7 – 20.46)/0.5 [As Z = (X-μ)/σ ]
= -1.52
For the upper limit (21.22 Ne):
Z_Upper = (21.22 – 20.46)/0.5
= 1.52

Now, we will use the cumulative distribution function (CDF) of the standard normal distribution to find the proportion of samples outside these z-scores.
The cumulative distribution function gives the area under the normal curve to the left of a given z-score.
For the lower limit:
P (below -1.52) = P (Z < -1.52)
For the upper limit:
P (above 1.52) = 1 – P (Z < 1.52)
Using a standard normal distribution table or calculator, we can find these probabilities:

• P (Z < -1.52) ≈ 0.063
• P (Z < 1.52) ≈ 0.935
  Now, we can find the off-count percentage:
  Off-count percentage = (0.063 + (1 – 0.935)* 100%)
  Off-count percentage = (0.063 + 0.065) *100 %
  Off-count percentage = 0.128 * 100%
  Off-count percentage = 12.8 %
  So, the off-count percentage is approximately 12.8%.