A manufacturing company produces knitted sports goods. It is found that 2% of the goods produced are defective. What is the probability that in a shipment of 100 such goods 4% or more will prove to be defective?

by

Answer:

To solve this problem, we can use the binomial probability distribution formula. The binomial distribution is applicable when there are two possible outcomes (defective or non-defective) and each trial is independent with a constant probability of success (defective in this case).

Let’s denote:

– (p) as the probability of a single item being defective (0.02 in this case).

– (n) as the number of trials (100 in this case).

– (X) as the number of defective items in the shipment.

We are interested in finding the probability that 4% or more of the goods in a shipment of 100 are defective. So, we need to find the probability of having 4 or more defective items, which can be represented as:

P(X ≥ 4) = P(X = 4) + P(X = 5) + …………+ P(X = 100)

We’ll use the binomial probability formula to calculate each of these probabilities and sum them up.

The binomial probability mass function is given by:

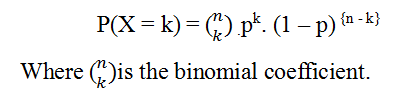
Let’s calculate this:

P(X ≥ 4) = P(X = 4) + P(X = 5) + …………+ P(X = 100)

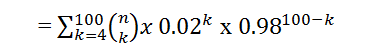
This sum can be computationally intensive to calculate directly. However, we can use statistical software or approximation methods. One common approximation method is to use the normal approximation to the binomial distribution

Let’s calculate (np) and n(1-p)

np = 100 x 0.02 = 2

n(1-p) = 100 x (1 – 0.02) = 98

Using the normal approximation, we can approximate the probability of having 4 or more defective items:

P(X ≥ 4) = 1 – P(X < 4)

Where P(X < 4) is the cumulative distribution function (CDF) of the normal distribution with mean ( μ = np) and standard deviation, σ = √{np (1-p)}

We can then use a standard normal distribution table or statistical software to find P(X < 4) and subtract it from 1 to find P(X ≥ 4)

Let calculate this.

μ = np = 100 * 0.02 = 2

σ = √{np (1-p} ≈ 1.4

Now, we’ll use these values to calculate the z-score for (X = 3), then use a standard normal distribution table or statistical software to find P(X < 4).

z = {X – μ)/ σ = 0.7143

Using a standard normal distribution table or statistical software, we find that P(X < 4) ≈ 0.7580

Now, we can find P(X ≥ 4)

P(X ≥ 4) = 1 – P(X < 4)

P(X ≥ 4) = 1 – 0.7580

P(X ≥ 4) = 0.2420

So, the probability that in a shipment of 100 goods, 4% or more will be defective is approximately 0.2420 or 24.20%.

Leave a Comment